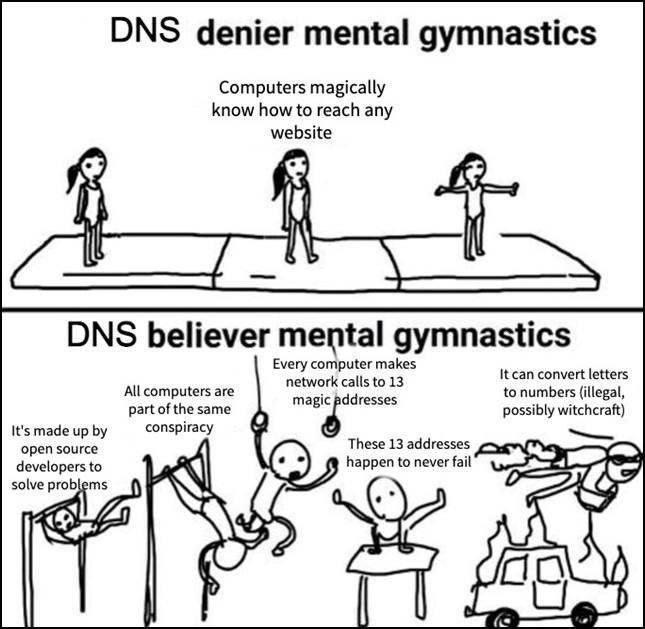
Physicist defining the fourier transformation vs Mathematicians

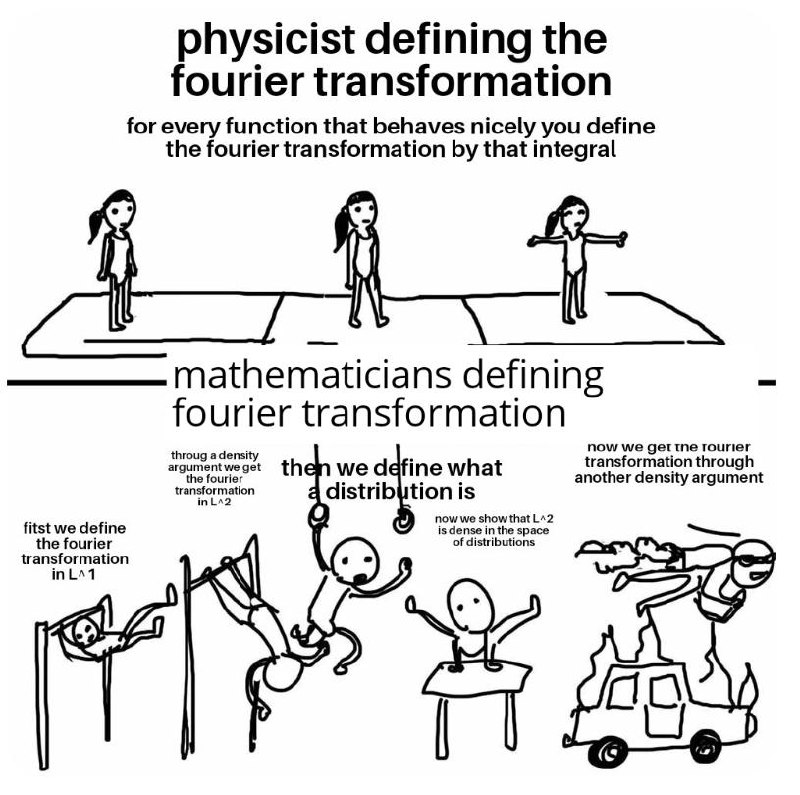
На картинке сравниваются подходы физиков и математиков к определению преобразования Фурье. Сверху показаны «физики», которые определяют преобразование Фурье простым интегралом для «каждой функции, которая ведет себя хорошо», демонстрируя расслабленный и упрощенный подход. В нижней части представлены «математики», которые проходят сложный и многоступенчатый процесс определения преобразования Фурье, начиная с L^1, затем переходя к L^2 через аргумент плотности, определяя распределение, доказывая плотность L^2 в пространстве распределений, и затем получая преобразование Фурье через другой аргумент плотности. Это подчеркивает их стремление к строгим и формальным определениям, даже если это требует значительно больше усилий и абстракций.

Physicist defining the fourier transformation. For every function that behaves nicely you define the fourier transformation by that integral. Mathematicians defining fourier transformation. Fitst we define the fourier transformation in L^1. Throug a density argument we get the fourier transformation in L^2. Then we define what a distribution is. Now we show that L^2 is dense in the space of distributions. Now we get the fourier transformation through another density argument.