Конические сечения и эксцентриситет e

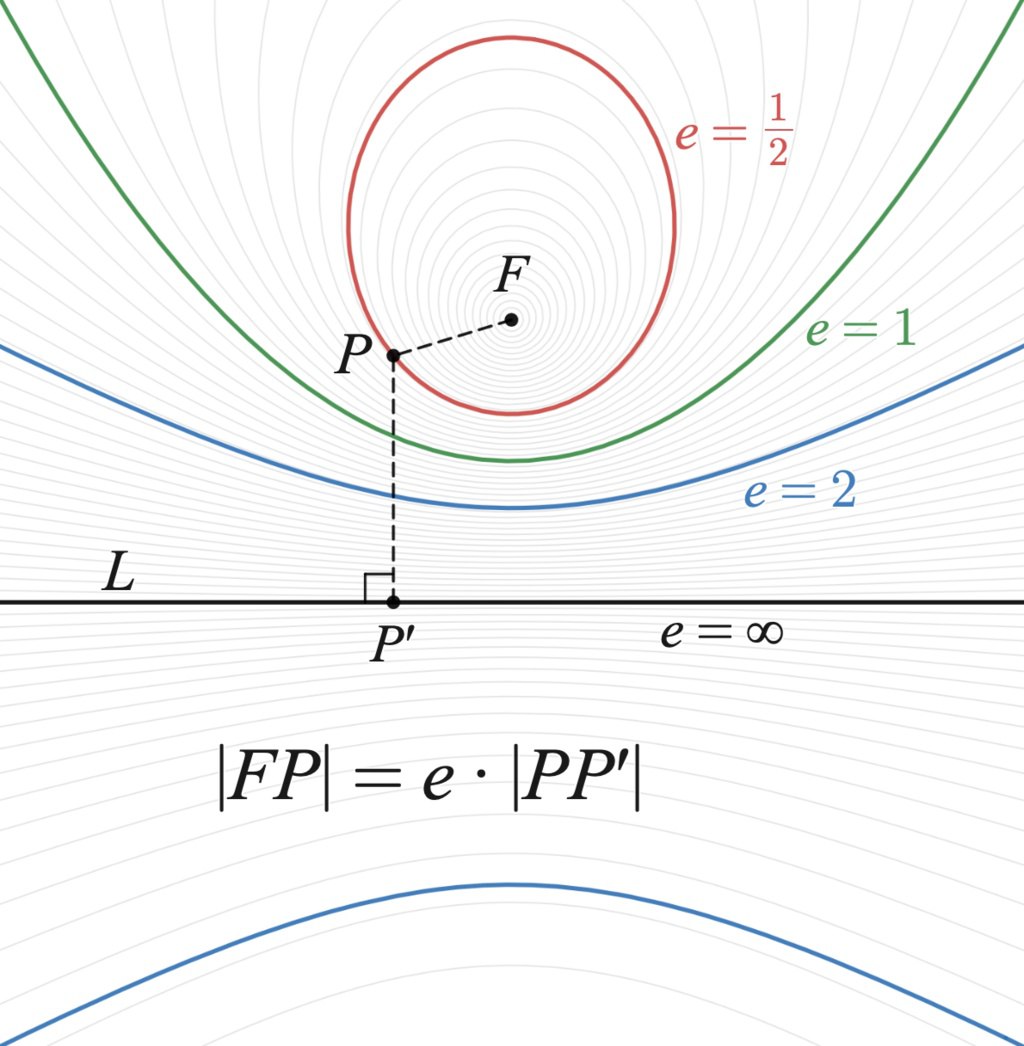
На изображении представлен геометрический чертеж, иллюстрирующий определение конических сечений с использованием эксцентриситета (e). Показаны различные кривые: красная эллипс (e = 1/2), зеленая парабола (e = 1) и синие гиперболы (e = 2 и e = ∞). Все кривые строятся относительно фокуса F и директрисы L. Точка P лежит на кривой, а P' - это проекция P на директрису L. Указано ключевое соотношение |FP| = e ⋅ |PP'|, которое является определением конических сечений: расстояние от точки на кривой до фокуса (FP) равно эксцентриситету (e), умноженному на расстояние от этой точки до директрисы (PP'). Это фундаментальная формула в геометрии.

e = 1/2. e = 1. e = 2. e = ∞. |FP| = e ⋅ |PP'|