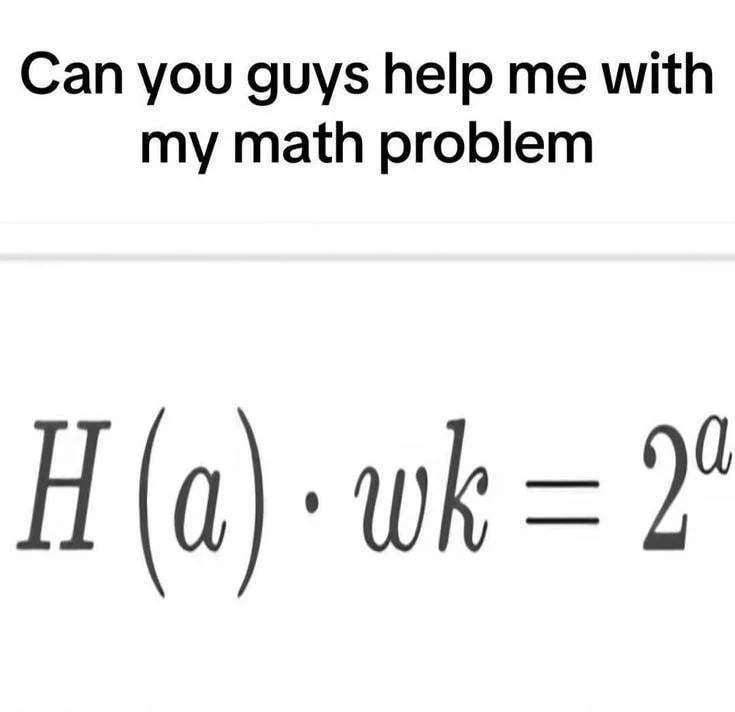Спросите ребёнка на улице

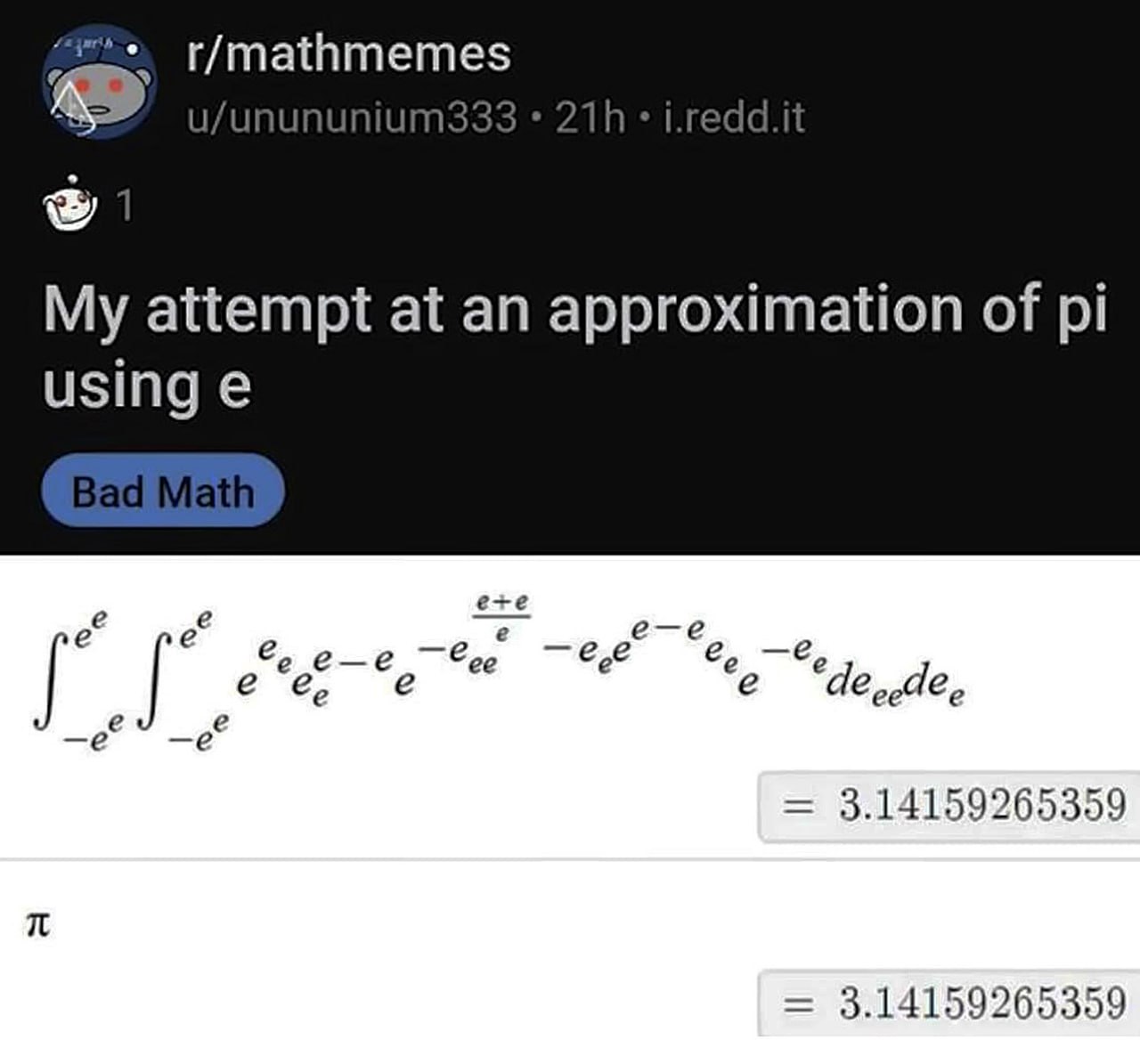
На изображении представлена страница из академического учебника, предположительно по высшей математике или алгебре, с множеством лемм и предложений. Каждое утверждение имеет свой номер (например, Lemma 1.1, Proposition 5.2, Lemma 6.1 и так далее) и содержит сложные математические формулы и определения. Однако, вместо традиционных строгих математических доказательств, под некоторыми леммами и предложениями в поле "Proof." (Доказательство.) написаны абсурдные или шуточные утверждения, выделенные жёлтым маркером. Например, "Proof. Well-known." (Доказательство. Хорошо известно.), "Proof. Ask a toddler on the street." (Доказательство. Спросите ребёнка на улице.), "Proof. Y'all are excellent number theorists. Do it yourselves." (Доказательство. Вы все отличные теоретики чисел. Сделайте это сами.), "Proof. Exercise." (Доказательство. Упражнение.), "Proof. Counterexample of minimal length and all that." (Доказательство. Контрпример минимальной длины и всё такое.). Эти "доказательства" контрастируют с серьёзностью и сложностью математических утверждений, создавая юмористический эффект и иронично подчёркивая трудность или очевидность некоторых концепций для опытных математиков.

Lemma 1.1. Every left kG-module gives rise to a unique representation of G over k and vice versa. Proof. Well-known. Lemma 5.1. Gal(K/Q) \cong (Z/mZ)*. Proof. Ask a toddler on the street. Proposition 5.2. OK/p is the smallest finite field containing the m-th roots of unity. If pr is the smallest power of p such that m | pr − 1, then: (i) OK/p \cong Fpr \to k. (ii) C + p \cong C. (iii) Gal(Fpr/Fp) is the stabiliser of p in Gal(K/Q). Proof. Y'all are excellent number theorists. Do it yourselves. Lemma 6.1. (i) \chi M(1) = dimk M. (ii) \chi M is a class function on p'-elements. (iii) \chi M(g−1) = \chi M(g) = \chi M*(g). (iv) If we have a short exact sequence 0 \to M1 \to M2 \to M3 \to 0 of finite-dimensional kG-modules, then \chi M2 = \chi M1 + \chi M3. In particular, \chi M depends only on the isomorphism class of M. (v) \chi M(g)\chi N(g) = \chi M\otimes N(g). Proof. Exercise. Lemma 6.9. Suppose R is a commutative ring and D is an integral domain, then every set of distinct ring homomorphisms R \to D is linearly independent over D. Proof. Counterexample of minimal length and all that. Lemma 8.1. The followings are equivalent: (i) P is projective. (ii) Every epimorphism \lambda : M \to P splits, i.e. there is a homomorphism \epsilon : P \to M such that \lambda \circ \epsilon = idP. (iii) P is isomorphic to a direct summand of a free R-module. Proof. Exercise.